Bilangan Kongruen

Meskipun mengunakan nama Kongkruen, bilangan kongkruen tidak ada hubungan (secara langsung) dengan relasi kongruen modul

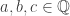Definsi: Suatu bilangan bulat positif  dikatakan bilangan kongruen jika merupakan nilai dari luas suatu segitiga siku-siku dengan panjang ketiga sisinya merupakan bilangan rasional, dengan kata lain terdapat sedemikian hingga  dan 

Contoh:

• 6 adalah kongruen dengan a=3, b=4 dan c=5
• 5 adalah kongruen dengan a=3/2, b=20/3 dan c=41/6
• 30 adalah kongruen dengan a=5, b=12 dan c=13

Nah…yang jadi pertanyaan adalah

Bagaimana mengetahui suatu bilangan bulat positif  adalah bilangan kongruen atau bukan?

Pertanyaan diatas dikenal dengan nama Masalah Bilangan Kongruen. Konon masalah tersebut sudah temuat dalam manuskrip arab yang ditulis oleh Matematikawan Persia Al-Karaji pada tahun 972. Akan tetapi baru bisa dijawab berabad-abad kemudian, oleh Teorema Tunnell pada tahun 1983.

Teorema Tunnell: Diberikan bilangan bulat positif  dan didefinisikan persamaan-persamaan berikut

JIka  adalah bilangan kongruen maka belaku

 untuk  ganjil

 untuk  genap.

Sebaliknya andaikan Dugaan Birch Swinnerton Dyer (DBSD) itu benar maka suatu yang memenuhi persamaan-persamaan diatas adalah bilangan Kongruen.

Teorema diatas mengasumsikan  DBSD benar, andaikan kelak DBSD terbukti salah maka Teorema Tunnell hanya berlaku setengah / separuh. Andaikan DBSD salah maka kita hanya bisa mengetahui bilangan kongruen pastilah memenuhi persamaan-persamaan pada Teorema Tunnel tetapi jika ada suatu  yang memenuhi persamaan-persamaan pada Teorema Tunnel, kita tidak bisa meyimpulkan  adalah bilangan kongruen.